My path to publishing my first app on the Google Play store has been a long one with odd beginnings. It all started when I first learned of simulated annealing algorithms from a post on hacker news months ago.  In that post someone was showing off their algorithm and how it could solve the Traveling Salesman Problem or some other tough NP-Complete problem. I can’t remember the specifics, but for whatever reason it inspired me to apply the technique to another NP-Complete problem: Sudoku puzzles!

I spent a couple weeks slowly working away at an implementation in Go and by the end had a configurable command line program that can reliably solve the easy puzzles, and sometimes also solve the harder ones. It doesn’t do that well on the “very hard” or “evil” Sudoku puzzles because they seem to branch early which creates excessively large peaks and troughs in the solution space that are insurmountable for my implementation. This could be because of my choice of cost function, or because I haven’t found the magic mix of parameters that maximize the likelihood of success. I incorporated some interesting tricks to the algorithm that I found while doing research; most notably the use of concurrent channels that run at exponentially increasing temperatures and thus have increasing likelihoods of escaping the deeper troughs in the search space. Each of these channels runs for a set number of iterations on their own, and then they return their current result and get compared to their neighbouring channels. Whenever a hotter channel has a better solution than a cooler channel they swap their current working solutions. The idea is that the hotter threads will keep the search from permanently getting stuck in a local minimum, while the cooler channels will inherit the best working solution and settle nicely into the minimum to find the solution if there is one.

This wasn’t the end of my Sudoku solving however. I started to wonder about deterministic algorithms for solving them and quickly stumbled onto Peter Norvig’s Constraint Propagation Search algorithm. I set to work implementing this algorithm in Go as well, and finished it not long after. The results were far more impressive than my simulated annealing algorithm: It always got the right solution, and typically in one tenth the time on even the hardest 9 x 9 puzzles I had in my test data.

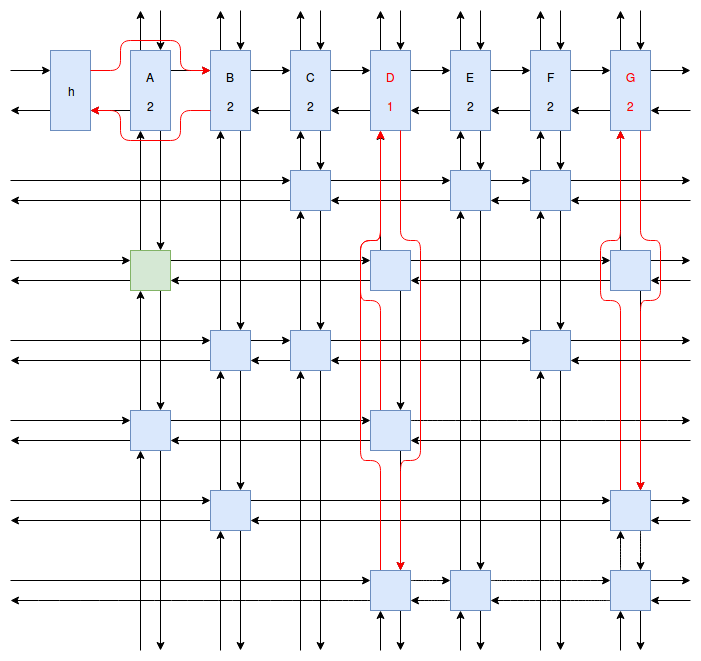
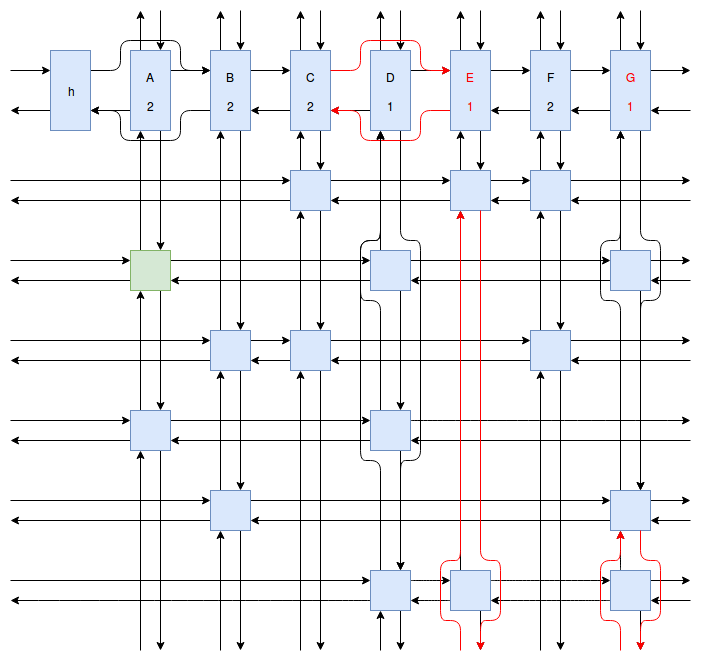
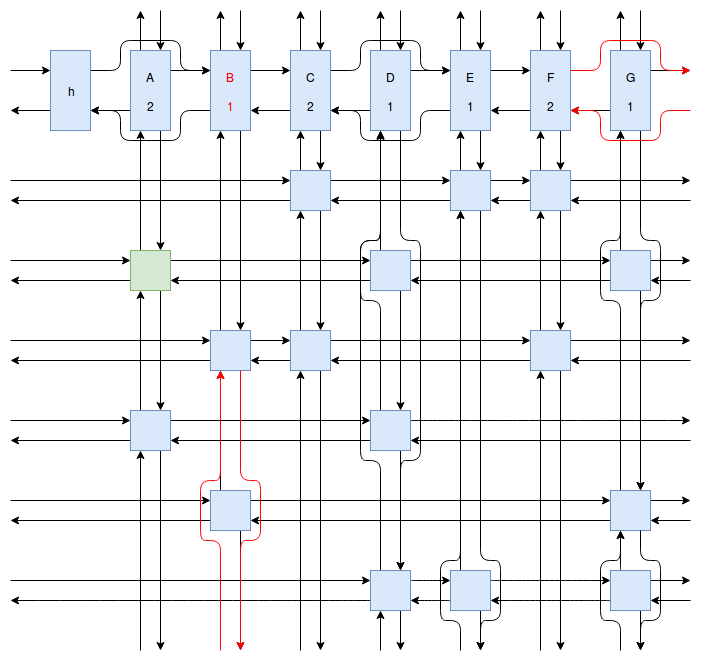
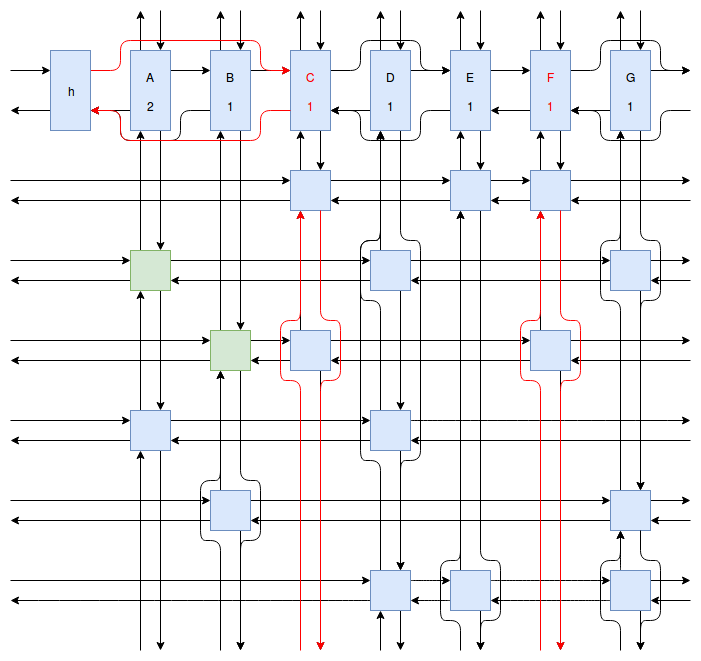
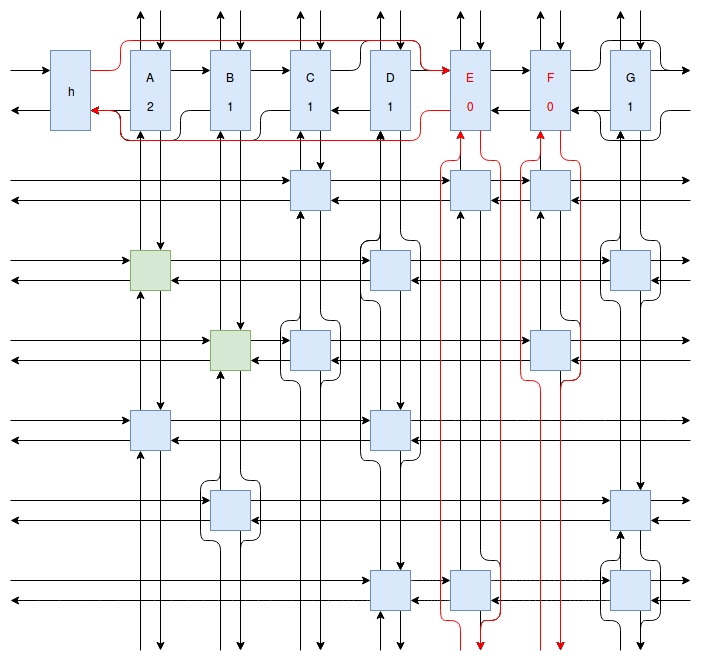
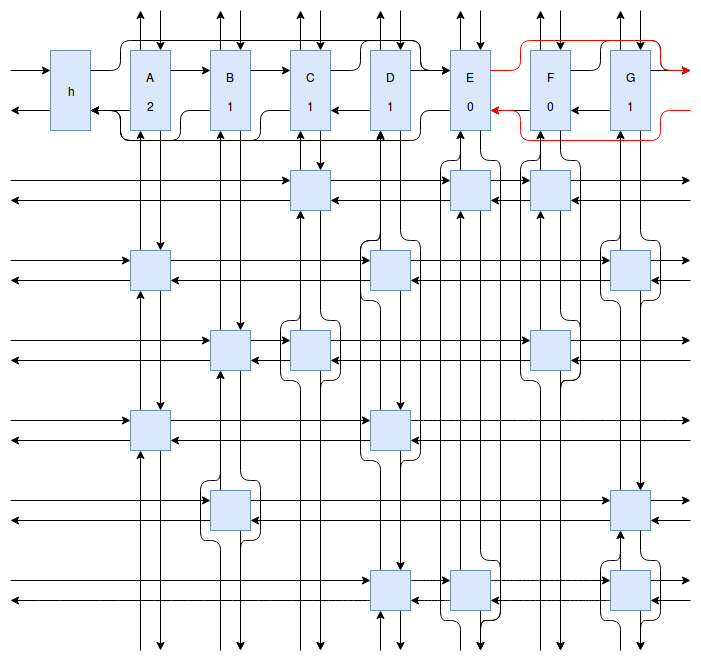
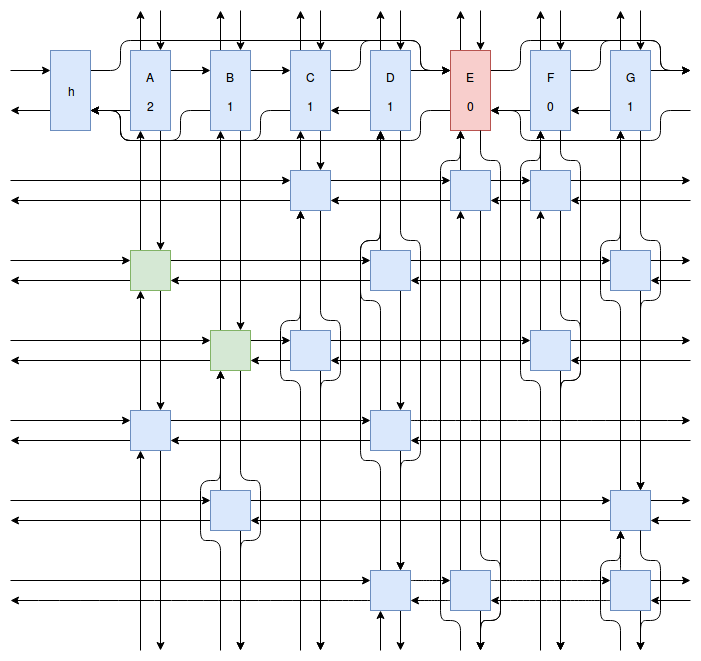
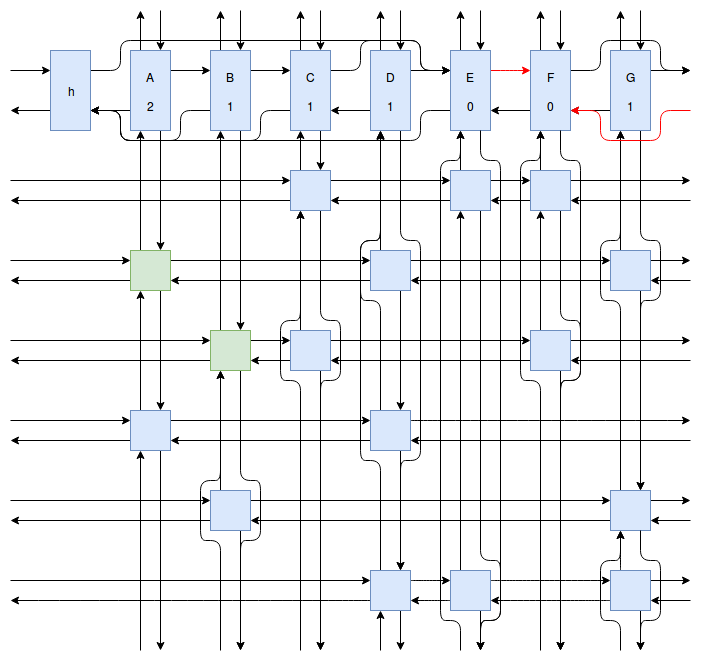
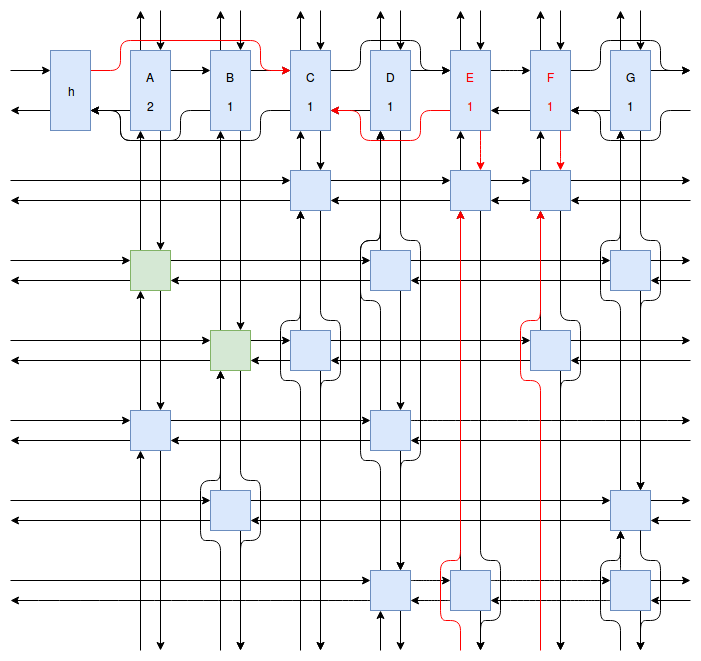
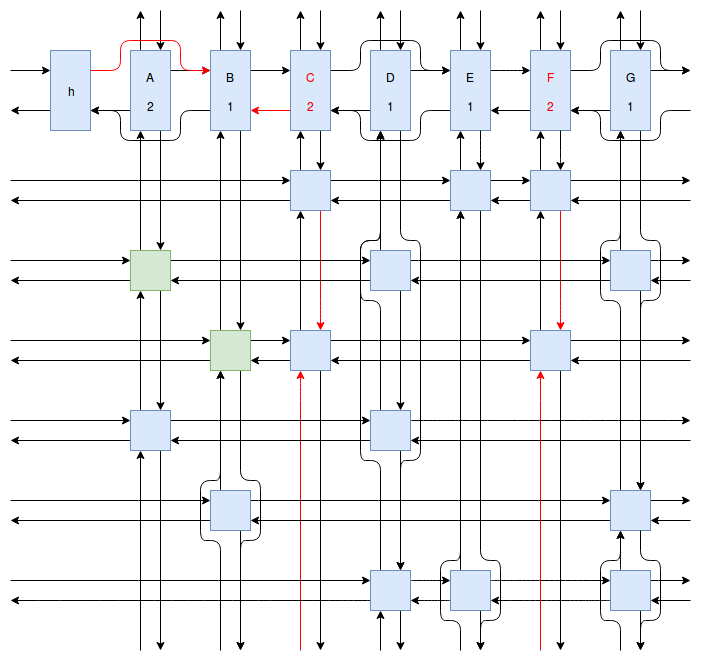
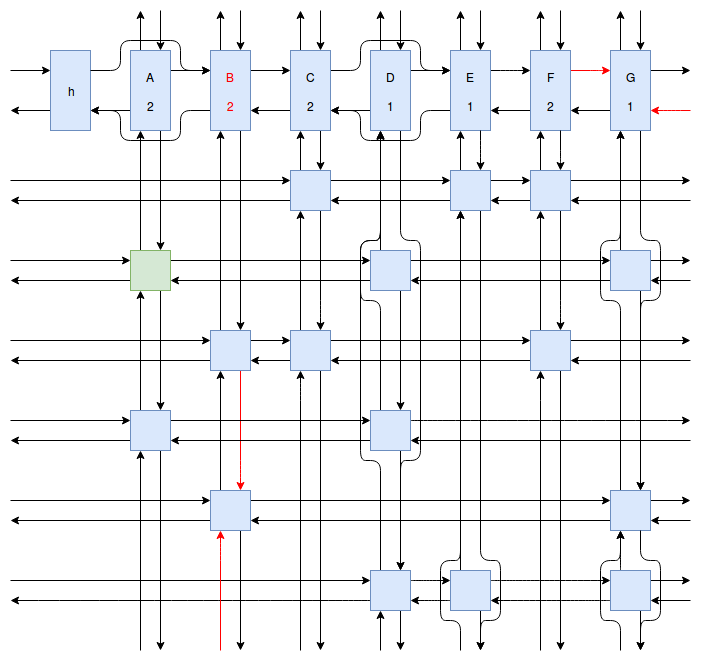
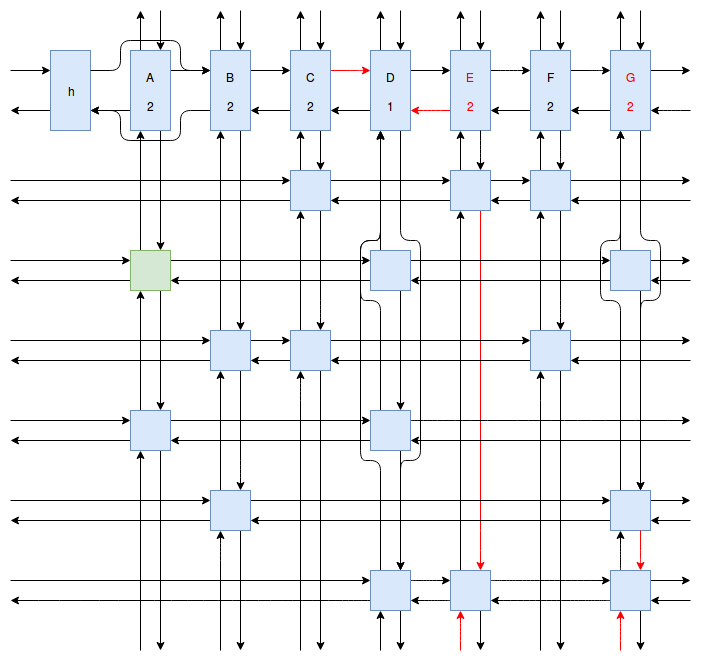
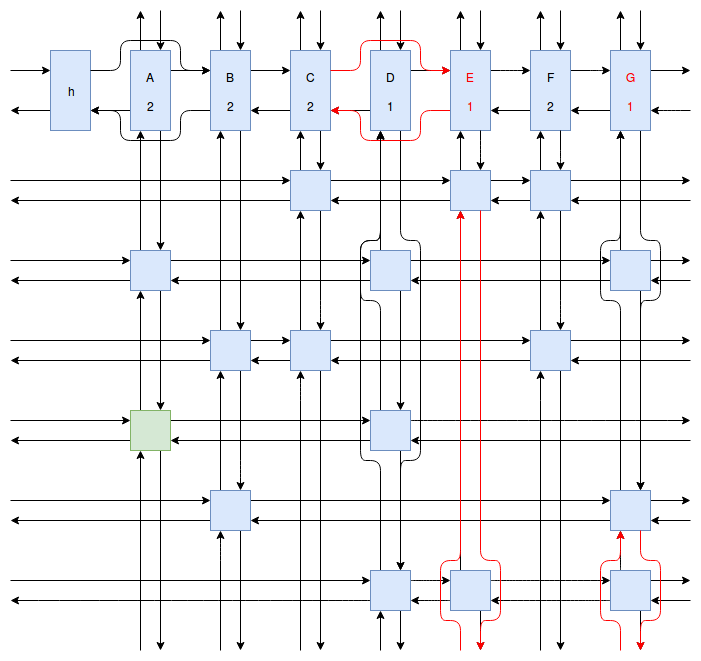
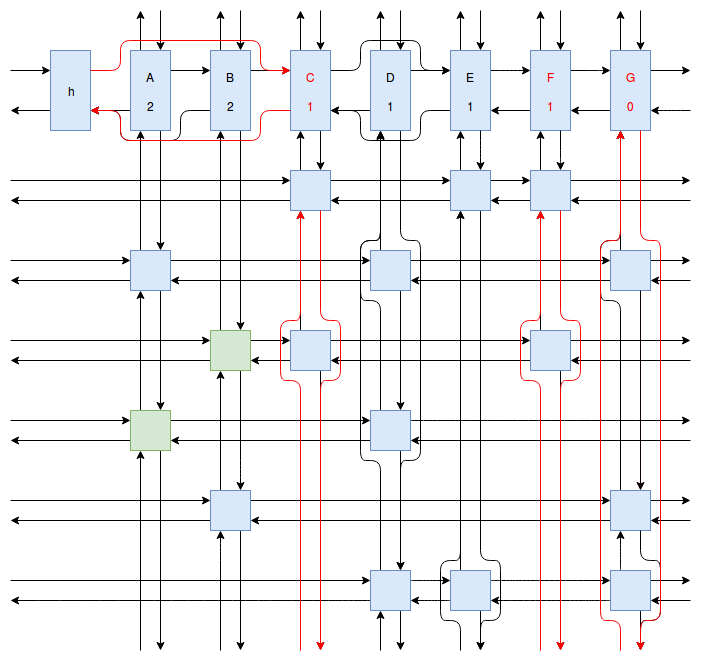
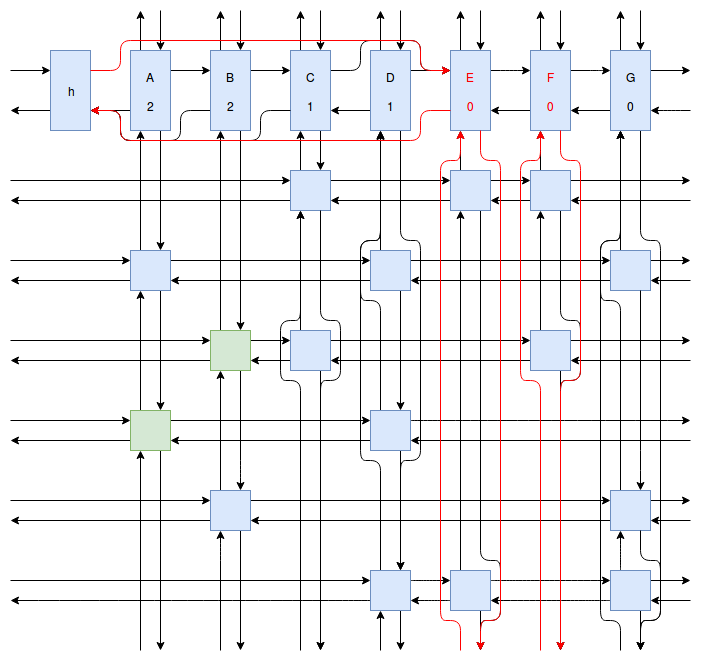
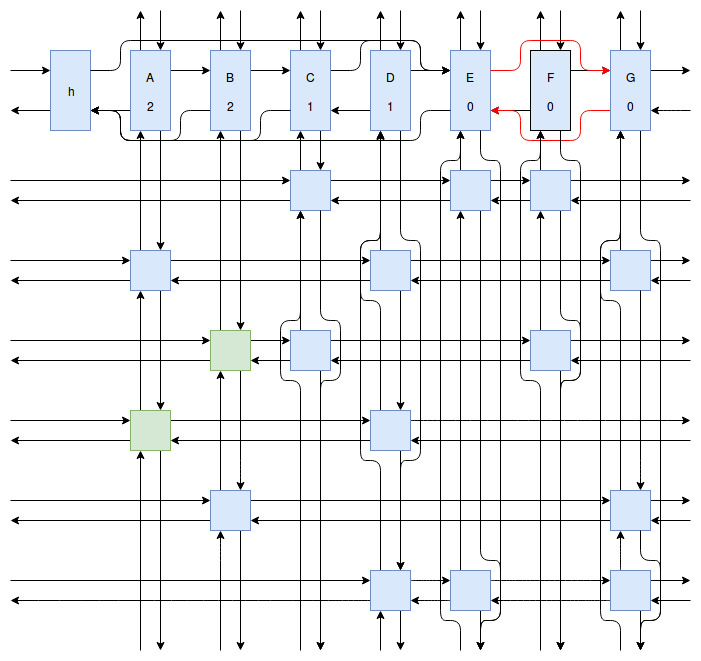
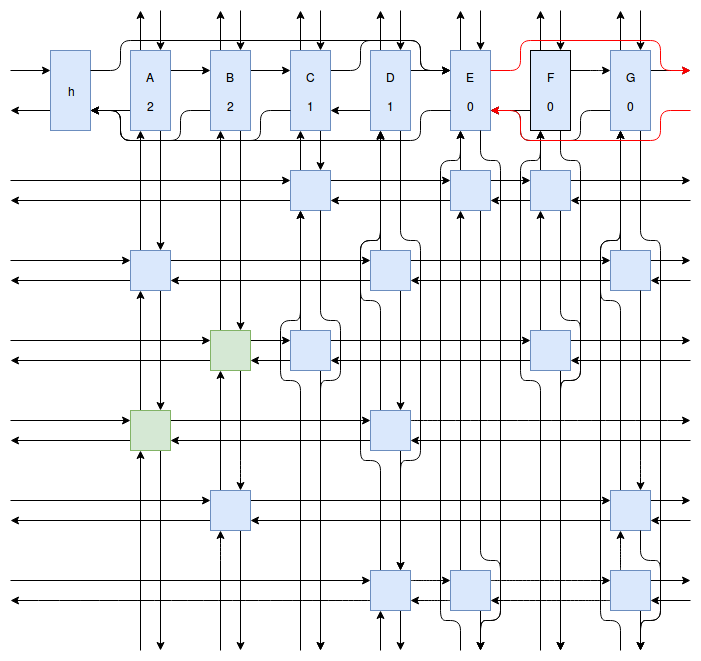
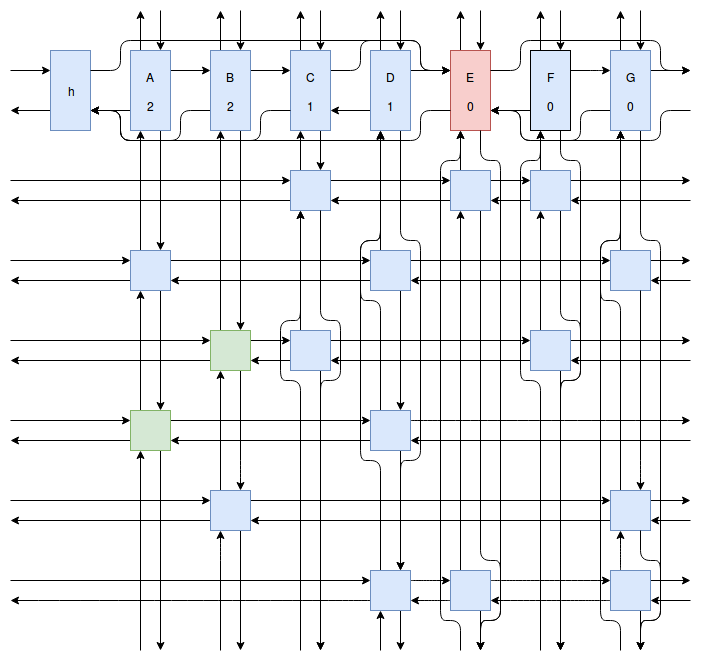
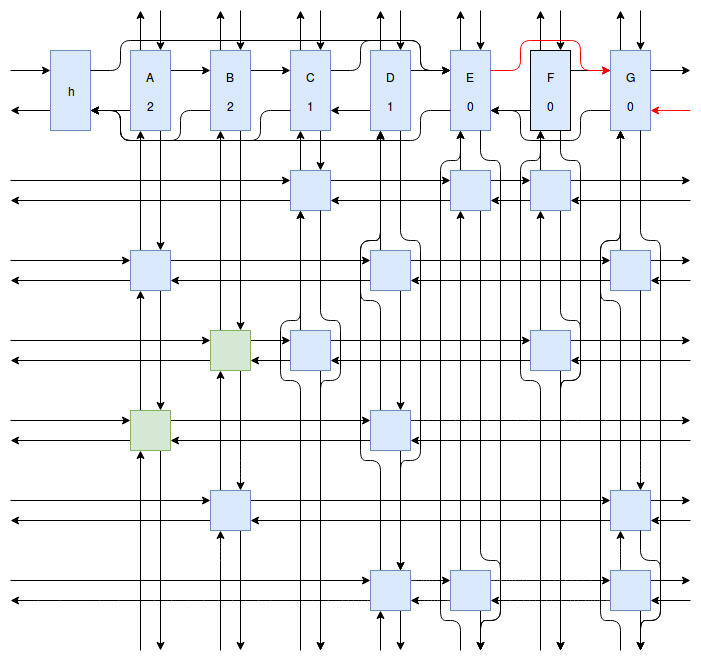
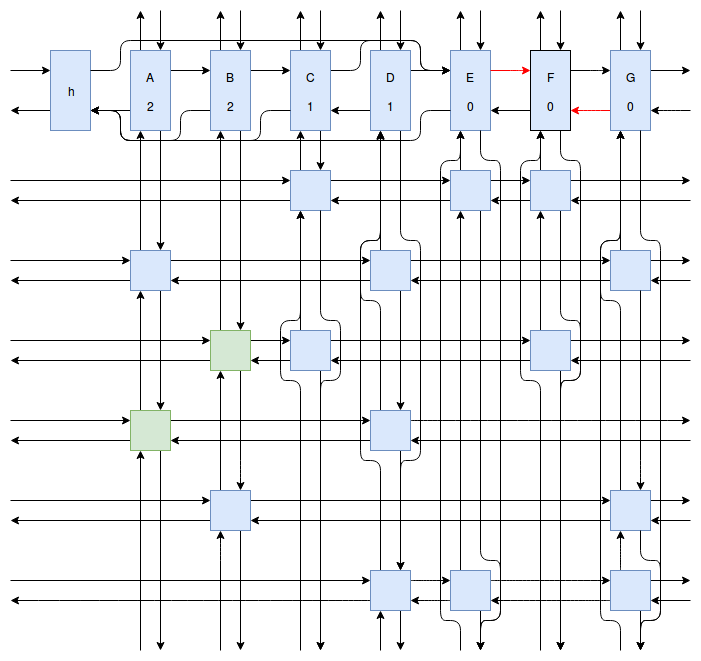
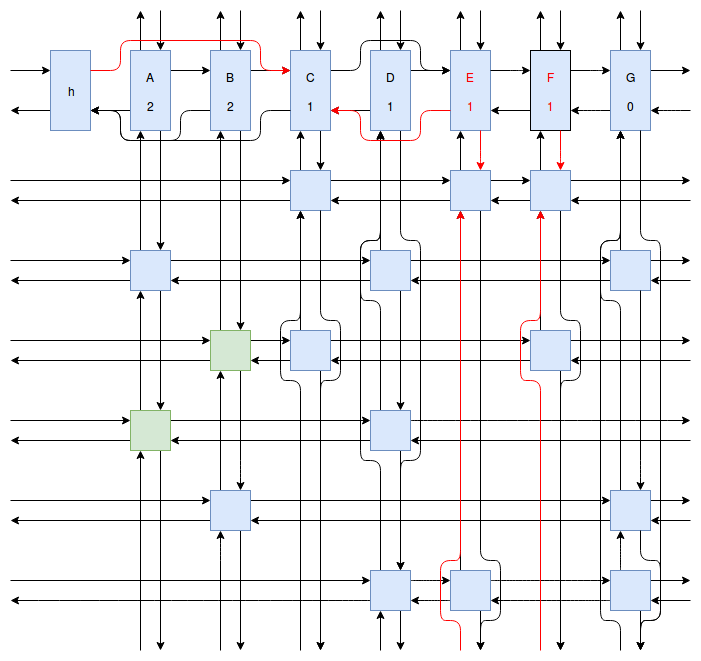
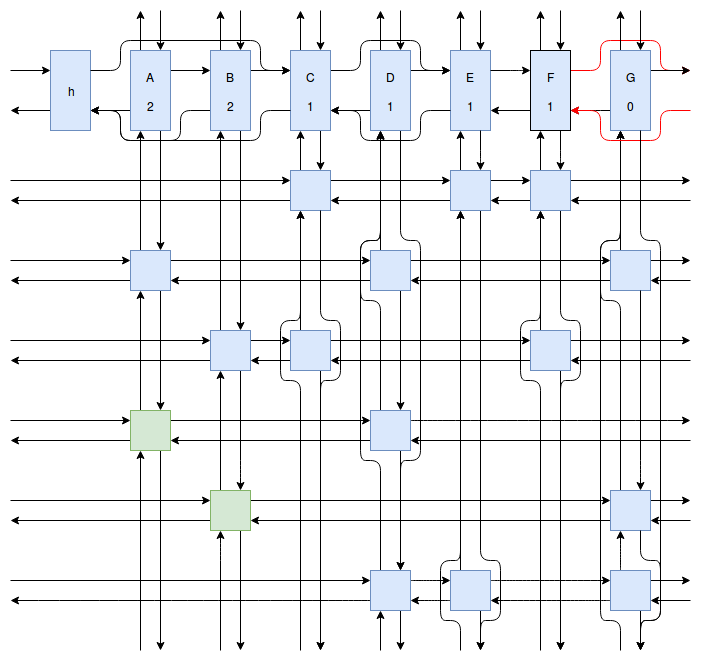
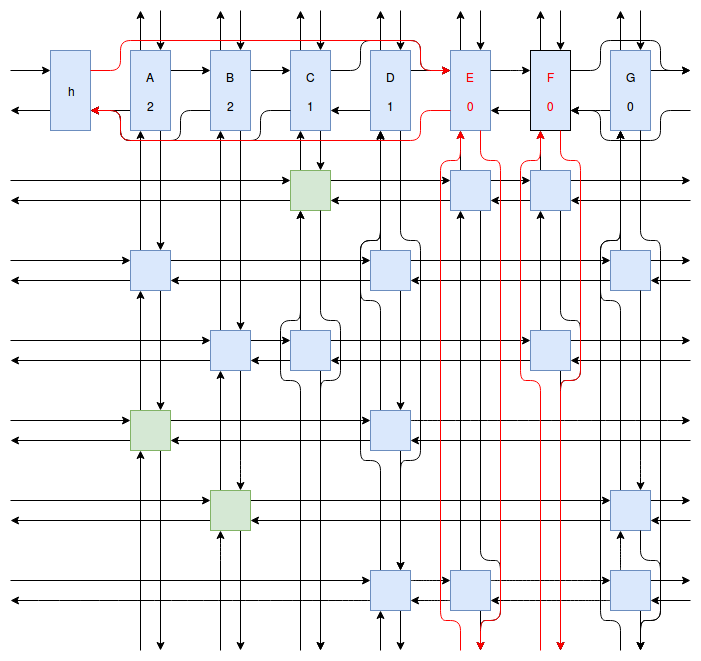
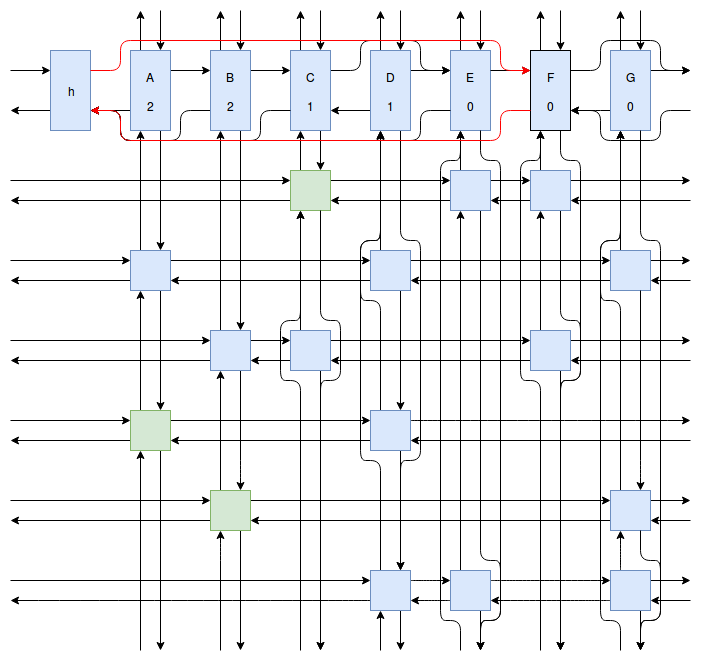
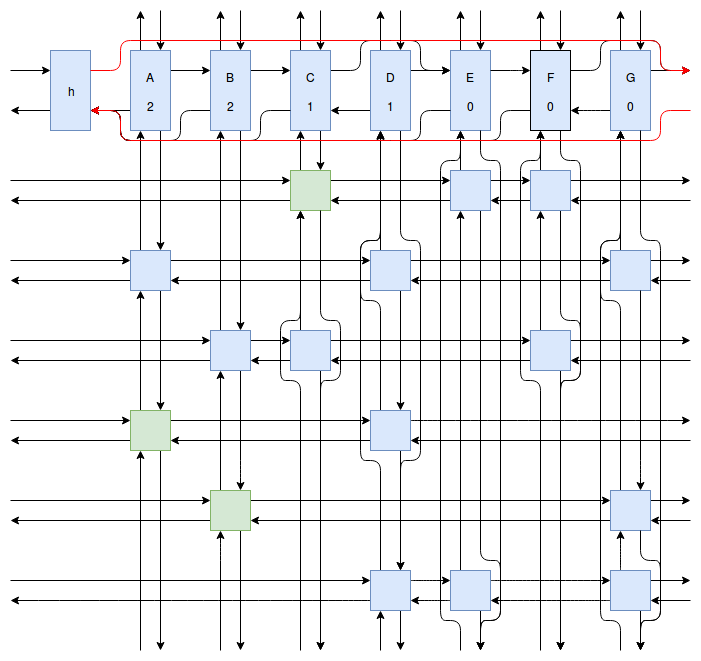
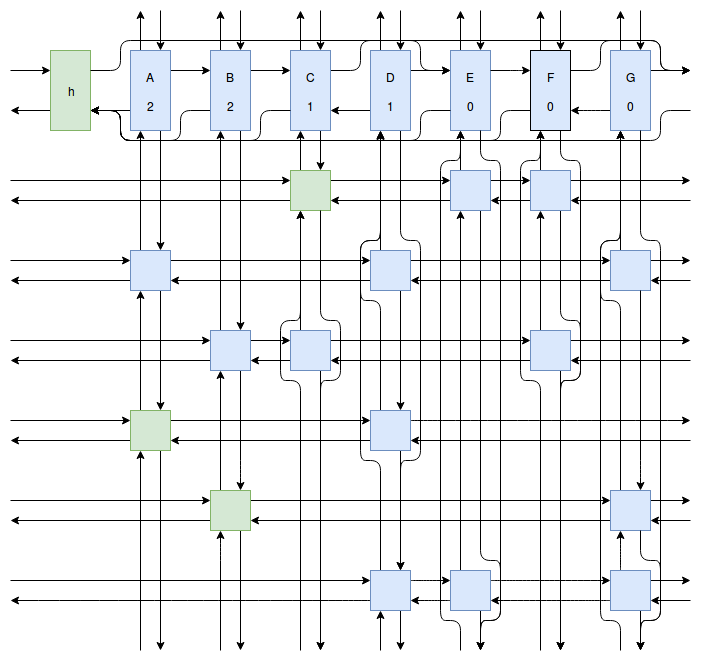
At this point my obsession with Sudoku solving algorithms was starting to peak, and I wanted to implement something even faster and more efficient than Peter Norvig’s algorithm. Eventually I stumbled onto Donald Knuth’s Dancing Links algorithm. At first I struggled to understand exactly how the algorithm worked. How could it be so much more efficient than Peter Norvig’s algorithm? It was obvious that Dancing Links avoids the computationally costly steps of copying the entire puzzle when a branch in the search space occurs, but I was still having trouble understanding how exactly it managed to backtrack and reverse the changes it made without copying. And so I spent far too much time drawing up the example problem in his paper using a flow charting web app.

Finally I understood it. I saw the dance occur right before my eyes, and no longer felt unworthy of applying it to my sudokus. And so I created another Go package called sudokuDlx. It manages to solve my sudoku puzzles much faster than the Constraint Propagation Search algorithm; it solves the full set of about 150 test puzzles in about half a second on my laptop versus more than 16 seconds for sudokuCPS. This advantage of speed is most noticeable when we attempt to solve Peter Norvig’s impossible puzzle. Here sudokuDlx determines the puzzle is impossible almost as fast as it takes to solve any valid puzzle while sudokuCPS takes an agonizing 10 minutes and 52 seconds to do the same task.

Having finished the Dancing Links implementation, I put the whole business of solving sudokus on hold. I spent most of the ensuing time on Udacity learning how to develop an android app. I sort of imagined trying to find some application for my new found sudoku solving skills when I started learning android development, but a major problem existed: Most android programs are written in Java, while all of my sudoku solvers are written in Go. I knew it would be possible to re-write the algorithms in Java, but I wasn’t super enthused about having to do that. I was almost prepared to find some other project to make into an android app, but decided to investigate Gomobile a little bit before giving up. It has quite a few limitations about the types and data structures that can be passed from Java to go and vice versa, but nothing that a few wrapper functions in the GO package can’t handle.

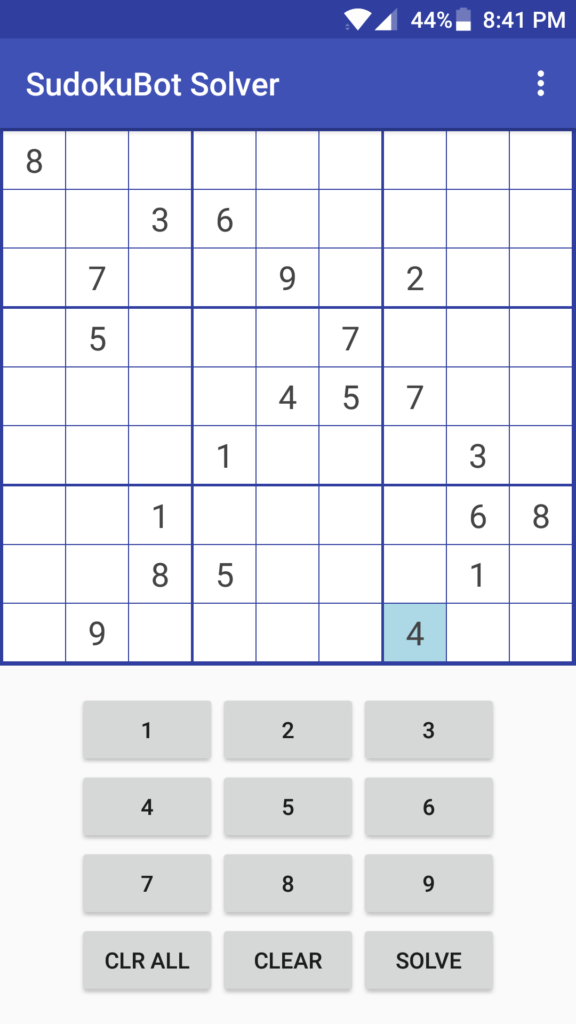
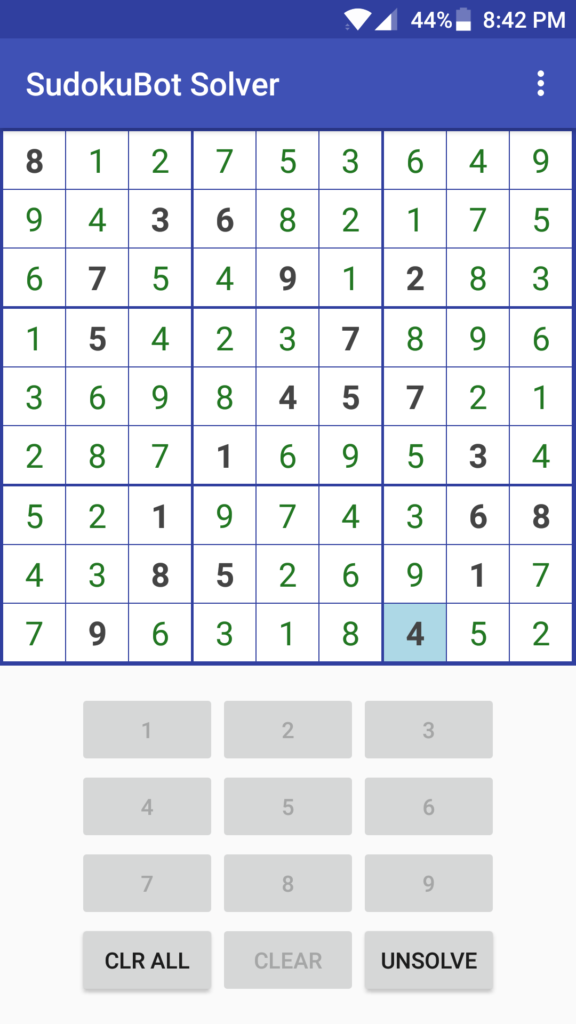
I set to work making my sudoku solving android app and after a couple dozen hours of development spread over evenings and weekends I finally have an app I feel is worth publishing. The code for this app is up on GitHub and the app itself can be downloaded on the Google Play store.